Adaptive optimized Schwarz methods
Conor McCoid
Felix Kwok
Université Laval

Schwarz methods
Consider the following sample problem: \[\Delta u(x,y) = f(x,y), \quad (x,y) \in \Omega = [-1,1] \times [-1,1]\] \[u(x,y)=h(x,y), \quad (x,y) \in \partial \Omega\]
We'll discretize this into
\[A \vec{u} = \vec{f}, \quad A \in \mathbb{R}^{N \times N}\]
\[A \vec{u} = \vec{f}, \quad A \in \mathbb{R}^{N \times N}\]
If $N$ is very large, this can take a long time to find $\vec{u}$
Schwarz methods divide the domain into smaller problems
Schwarz methods divide the domain into smaller problems
\[\Delta u_1^n(x,y) = f(x,y), \quad (x,y) \in \Omega_1 = [-1,\alpha] \times [-1,1]\] \[u_1^n(\alpha,y)=u_2^{n-1}(\alpha,y)\] \[\Delta u_2^n(x,y) = f(x,y), \quad (x,y) \in \Omega_2 = [\beta,1] \times [-1,1]\] \[u_2^n(\beta,y)=u_1^{n-1}(\beta,y)\]
Schwarz methods divide the domain into smaller problems
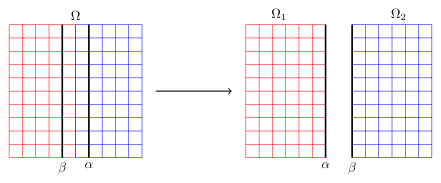
Schwarz methods divide the domain into smaller problems
Multiplicative Schwarz: solve one subdomain after the other
Additive Schwarz: solve both subdomains at the same time
Schwarz methods divide the domain into smaller problems
\[\begin{bmatrix} A_{11} & A_{1\Gamma} \\ A_{\Gamma 1} & A_{\Gamma \Gamma} & A_{\Gamma 2} \\ & A_{2 \Gamma} & A_{22} \end{bmatrix} \begin{bmatrix} \vec{u}_1 \\ \vec{u}_\Gamma \\ \vec{u}_2 \end{bmatrix} = \begin{bmatrix} \vec{f}_1 \\ \vec{f}_\Gamma \\ \vec{f}_2 \end{bmatrix}\]
Schwarz methods divide the domain into smaller problems
\[\begin{bmatrix} A_{11} & A_{1 \Gamma} \\ A_{\Gamma 1} & A_{\Gamma \Gamma} + T_{2 \to 1} \end{bmatrix} \begin{bmatrix} \vec{u}_1^{n+1} \\ \vec{u}_{1 \Gamma}^{n+1} \end{bmatrix} = \begin{bmatrix} \vec{f}_1 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 2} \vec{u}_2^n + T_{2 \to 1} \vec{u}_{2 \Gamma}^n \end{bmatrix}\] \[\begin{bmatrix} A_{22} & A_{2 \Gamma} \\ A_{\Gamma 2} & A_{\Gamma \Gamma} + T_{1 \to 2} \end{bmatrix} \begin{bmatrix} \vec{u}_2^{n+1} \\ \vec{u}_{2 \Gamma}^{n+1} \end{bmatrix} = \begin{bmatrix} \vec{f}_2 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 1} \vec{u}_1^n + T_{1 \to 2} \vec{u}_{1 \Gamma}^n \end{bmatrix}\]
Optimized Schwarz methods
Boundary conditions transmit information between the two subdomains
We've used Dirichlet BCs
We could use Robin BCs instead
We could use Robin BCs instead
\[\Delta u_1^n(x,y) = f(x,y), \quad (x,y) \in \Omega_1 = [-1,0] \times [-1,1]\] \[\frac{\partial u_1^n}{\partial x} - p u_1^n(0,y)= \frac{\partial u_2^{n-1}}{\partial x} - p u_2^{n-1}(0,y)\] \[\Delta u_2^n(x,y) = f(x,y), \quad (x,y) \in \Omega_2 = [0,1] \times [-1,1]\] \[\frac{\partial u_2^n}{\partial x} - p u_2^n(0,y)= \frac{\partial u_1^{n-1}}{\partial x} - p u_1^{n-1}(0,y)\]
We could use Robin BCs instead
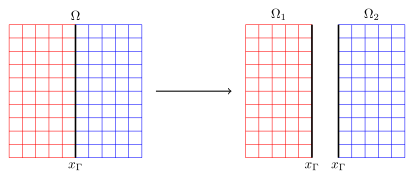
Now there's a choice in Robin parameter $p$, and this choice can be optimized
Optimization is done using Fourier analysis and finds the best $p$ for all Fourier modes
If you have a specific Fourier mode in mind, you can also pick the best $p$ for just that mode
Robin BCs aren't the only option for optimized BCs
Tangential BCs are also a popular choice, and give a second parameter $q$ to optimize \[\frac{\partial u_1^n}{\partial x} - p u_1^n(0,y) + q \frac{\partial u_1^n}{\partial y}=\] \[\frac{\partial u_2^{n-1}}{\partial x} - p u_2^{n-1}(0,y) + q \frac{\partial u_2^n}{\partial y}\]
But the best BCs are absorbing BCs, which are used in perfectly matched layers
These are dense, and correspond to Schur complements \[T_{2 \to 1} \to S_{2 \to 1} = -A_{\Gamma 2} A_{22}^{-1} A_{2 \Gamma},\] \[T_{1 \to 2} \to S_{1 \to 2} = -A_{\Gamma 1} A_{11}^{-1} A_{1 \Gamma}\]
These are dense, and correspond to Schur complements \[T_{2 \to 1} \to S_{2 \to 1} = -A_{\Gamma 2} A_{22}^{-1} A_{2 \Gamma},\] \[T_{1 \to 2} \to S_{1 \to 2} = -A_{\Gamma 1} A_{11}^{-1} A_{1 \Gamma}\]
This means they have about the same computation time as $M$ iterations, where $M$ is the size of the overlap
Adaptive transmission conditions
Finding optimized BCs requires Fourier analysis on each given problem
And the optimal BCs need Schur complements which are expensive to calculate
We want cheap, black box BCs
To get them, we'll find them adaptively
Let's look at the differences between iterates for a single sudomain
\[ \begin{bmatrix} A_{11} & A_{1 \Gamma} \\ A_{\Gamma 1} & A_{\Gamma \Gamma} + T_{2 \to 1} \end{bmatrix} \left ( \begin{bmatrix} \vec{u}_1^{n+1} \\ \vec{u}_{1 \Gamma}^{n+1} \end{bmatrix} - \begin{bmatrix} \vec{u}_1^n \\ \vec{u}_{1 \Gamma}^n \end{bmatrix} \right ) = \]\[ \begin{bmatrix} \vec{f}_1 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 2} \vec{u}_2^n + T_{2 \to 1} \vec{u}_{2 \Gamma}^n \end{bmatrix} - \left (\begin{bmatrix} \vec{f}_1 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 2} \vec{u}_2^{n-1} + T_{2 \to 1} \vec{u}_{2 \Gamma}^{n-1} \end{bmatrix} \right ) \]
Let's look at the differences between iterates for a single sudomain
\[ \begin{bmatrix} A_{11} & A_{1 \Gamma} \\ A_{\Gamma 1} & A_{\Gamma \Gamma} + T_{2 \to 1} \end{bmatrix} \begin{bmatrix} \vec{d}_1^{n+1} \\ \vec{d}_{1 \Gamma}^{n+1} \end{bmatrix} = \]\[ \begin{bmatrix} ~ \\ -A_{\Gamma 2} \vec{d}_2^n + T_{2 \to 1} \vec{d}_{2 \Gamma}^n \end{bmatrix} \]
We then perform what's known as static condensation by noting that \[A_{11} \vec{d}_1^{n+1} = -A_{\Gamma 1} \vec{d}_{1 \Gamma}^{n+1} \]
This leads to
\[(A_{\Gamma \Gamma} + S_{1 \to 2} + T_{2 \to 1}) \vec{d}_{1 \Gamma}^{n+1} = (T_{2 \to 1} - S_{2 \to 1}) \vec{d}_{2 \Gamma}^n \]
\[ \vec{y}^{n+1} = E_2 \vec{d}_{2 \Gamma}^n = -A_{\Gamma 2} \vec{d}_2^n + T_{2 \to 1} \vec{d}_{2 \Gamma}^n \]
\[ \vec{y}^{n+1} = E_2 \vec{d}_{2 \Gamma}^n = -A_{\Gamma 2} \vec{d}_2^n + T_{2 \to 1} \vec{d}_{2 \Gamma}^n \]
At every other iteration, we're going to update $E_2$
\[ E_2 \to E_2 - \frac{ \vec{y} \vec{d}^\top }{ \Vert \vec{d} \Vert^2 } \]
\[ E_2 \to E_2 - \frac{ \vec{y} \vec{d}^\top }{ \Vert \vec{d} \Vert^2 } \]
With each iteration, there's a new pair of $\vec{y}$ and $\vec{d}$
We can apply a modified Gram-Schmidt process to the vectors $\vec{d}$, making the vectors $\vec{w}$
Through this process, the vectors $\vec{y}$ get modified as well, to the vectors $\vec{v}$
\[ E_2 \to E_2 - V W^\top \]
Since $V = E_2 W$, this is equivalent to \[ E_2 \to E_2 \left ( I - W W^\top \right ) \]
We generate a low rank approximation of $E_2$
To make the optimized BCs, we subtract this from $T_{2 \to 1}$
The transmission conditions $T_{2 \to 1}$ and $T_{1 \to 2}$ now change iteratively

Recall: \[(A_{\Gamma \Gamma} + S_{1 \to 2} + T_{2 \to 1}) \vec{d}_{1 \Gamma}^{n+1} = (T_{2 \to 1} - S_{2 \to 1}) \vec{d}_{2 \Gamma}^n \]
The vectors $\vec{d}$ lie in a Krylov subspace
They satisfy an implicit Galerkin condition
There's also the option to update the BCs at every iteration

Adaptive Optimized Schwarz Methods (AOSMs)
1. Initial guesses
Make initial choices of $\vec{u}_{1 \Gamma}^0$, $T_{1 \to 2}^1$ and $T_{2 \to 1}^1$
Find $\vec{u}_1^0 = A_{11}^{-1} \left ( \vec{f}_1 - A_{1 \Gamma} \vec{u}_{1 \Gamma}^0 \right )$
Solve \[ \begin{bmatrix} A_{22} & A_{2 \Gamma} \\ A_{\Gamma 2} & A_{\Gamma \Gamma} + T_{1 \to 2}^1 \end{bmatrix} \begin{bmatrix} \vec{u}_{2}^1 \\ \vec{u}_{2 \Gamma}^1 \end{bmatrix} = \begin{bmatrix} \vec{f}_2 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 1} \vec{u}_1^0 + T_{1 \to 2}^1 \vec{u}_{1 \Gamma}^0 \end{bmatrix} \]
2. Seed Krylov subspace
Solve \[ \begin{bmatrix} A_{11} & A_{1 \Gamma} \\ A_{\Gamma 1} & A_{\Gamma \Gamma} + T_{2 \to 1}^1 \end{bmatrix} \begin{bmatrix} \vec{u}_{1}^2 \\ \vec{u}_{1 \Gamma}^2 \end{bmatrix} = \begin{bmatrix} \vec{f}_1 \\ \vec{f}_\Gamma \end{bmatrix} + \begin{bmatrix} ~ \\ -A_{\Gamma 2} \vec{u}_2^1 + T_{2 \to 1}^1 \vec{u}_{2 \Gamma}^1 \end{bmatrix} \]
Calculate $\vec{d}_{1 \Gamma}^2 = \vec{u}_{1 \Gamma}^2 - \vec{u}_{1 \Gamma}^0$ and $\vec{d}_{1}^2 = \vec{u}_{1}^2 - \vec{u}_{1}^0$
2. Seed Krylov subspace
Calculate $\vec{d}_{1 \Gamma}^2 = \vec{u}_{1 \Gamma}^2 - \vec{u}_{1 \Gamma}^0$ and $\vec{d}_{1}^2 = \vec{u}_{1}^2 - \vec{u}_{1}^0$
Normalize $\vec{d}_{1 \Gamma}^2$ using $\alpha_1^2$ such that $\vec{w}_1^2 = \alpha_1^2 \vec{d}_{1 \Gamma}^2$ and calculate \[ \vec{v}_1^2 = \alpha_1^2 \left ( -A_{\Gamma 1} \vec{d}_1^2 + T_{1 \to 2}^1 \vec{d}_{1 \Gamma}^2 \right ) \]
Update $T_{1 \to 2}^1$: \[ T_{1 \to 2}^2 = T_{1 \to 2}^1 + \Delta T_{1 \to 2}^2 = T_{1 \to 2}^1 - \vec{v}_1^2 \left ( \vec{w}_1^2 \right )^\top \]
2. Seed Krylov subspace
Solve
\[ \begin{bmatrix} A_{22} & A_{2 \Gamma} \\ A_{\Gamma 2} & A_{\Gamma \Gamma} + T_{1 \to 2}^2 \end{bmatrix} \begin{bmatrix} \vec{d}_{2}^3 \\ \vec{d}_{2 \Gamma}^3 \end{bmatrix} \]
\[ = \begin{bmatrix} ~ \\ -A_{\Gamma 1} \vec{d}_1^2 + T_{1 \to 2}^2 \vec{d}_{1 \Gamma}^2 - \Delta T_{1 \to 2}^2 \left ( \vec{u}_{2 \Gamma}^1 - \vec{u}_{1 \Gamma}^0 \right ) \end{bmatrix} \]
2. Seed Krylov subspace
Solve
\[ \begin{bmatrix} A_{22} & A_{2 \Gamma} \\ A_{\Gamma 2} & A_{\Gamma \Gamma} + T_{1 \to 2}^2 \end{bmatrix} \begin{bmatrix} \vec{d}_{2}^3 \\ \vec{d}_{2 \Gamma}^3 \end{bmatrix} \]
\[ = \langle \vec{w}_1^2, \vec{u}_{2 \Gamma}^1 - \vec{u}_{1 \Gamma}^0 \rangle \begin{bmatrix} ~ \\ \vec{v}_1^2 \end{bmatrix} \]
2. Seed Krylov subspace
Normalize $\vec{d}_{2 \Gamma}^3$ using $\alpha_2^3$ such that $\vec{w}_2^3 = \alpha_2^3 \vec{d}_{2 \Gamma}^3$ and calculate \[ \vec{v}_2^3 = \alpha_2^3 \left ( -A_{\Gamma 2} \vec{d}_2^3 + T_{2 \to 1}^1 \vec{d}_{2 \Gamma}^3 \right ) \]
Update $T_{2 \to 1}^1$: \[ T_{2 \to 1}^3 = T_{2 \to 1}^1 - \vec{v}_2^3 \left ( \vec{w}_2^3 \right )^\top \]
3. Iterate
Solve for $\vec{d}_i^n$ and $\vec{d}_{i \Gamma}^n$
Apply modified Gram-Schmidt to find $\vec{v}_i^n$ and $\vec{w}_i^n$
Update $T_{i \to j}^n$ using $\vec{v}_i^n \left ( \vec{w}_i^n \right )^\top$
Woodbury matrix identity
The updates to $T_{1 \to 2}^n$ and $T_{2 \to 1}^n$ are low rank
In order to preserve any matrix factorizations, we can use the Woodbury matrix identity to apply these low rank updates
\[(A - V W^\top) \vec{u} = \vec{f},\] \[\vec{u} = A^{-1} \vec{f} + A^{-1} V (I_{k \times k} - W^\top A^{-1} V)^{-1} W^\top A^{-1} \vec{f}\]
Numerical experiments
Recall the sample problem: \[\Delta u(x,y) = f(x,y), \quad (x,y) \in \Omega = [-1,1] \times [-1,1]\] \[u(x,y)=h(x,y), \quad (x,y) \in \partial \Omega\]
Let's apply AOSMs to this problem
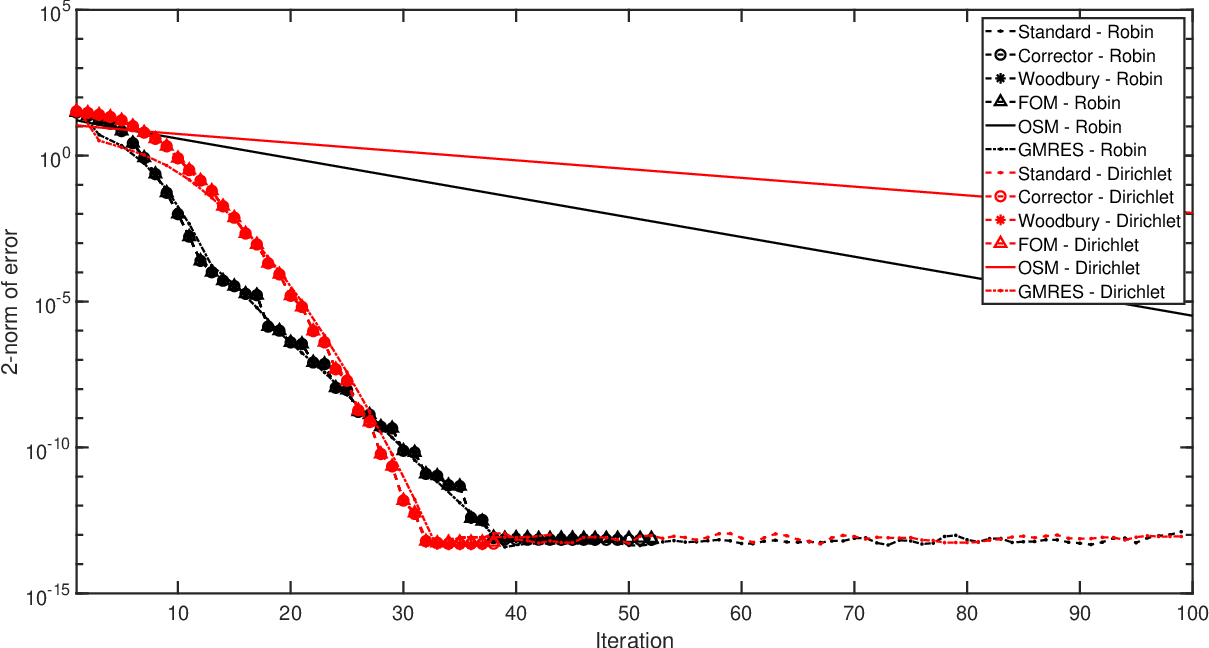
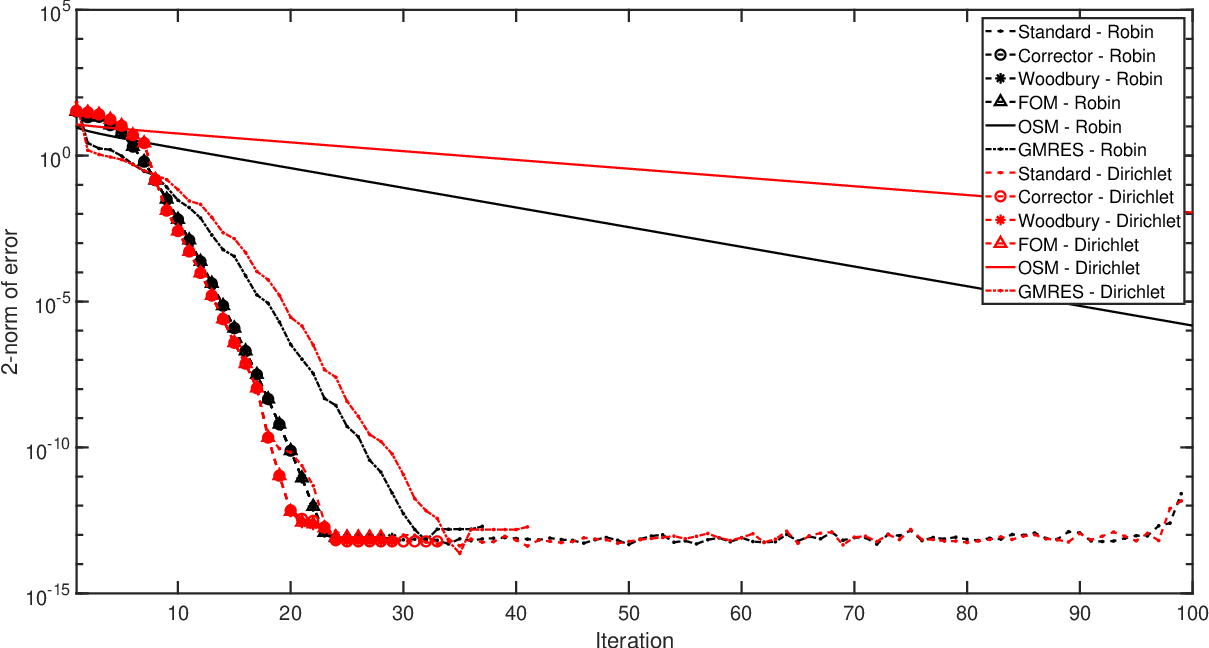
\[ u_t(x,y,t) = \Delta u(x,y,t), \quad (x,y) \in \Omega = [-1,1] \times [-1,1], \ t \in [0,T] \] \[ u(x,y,0) = u_0(x,y), \quad (x,y) \in \Omega, \] \[ u(x,y,t) = h(x,y), \quad (x,y) \in \partial \Omega, \ t \in [0,T] \]
\[\frac{u_{n+1} - u_n}{\Delta t} = A u_{n+1}\] \[(I - \Delta t A) u_{n+1} = u_n\]
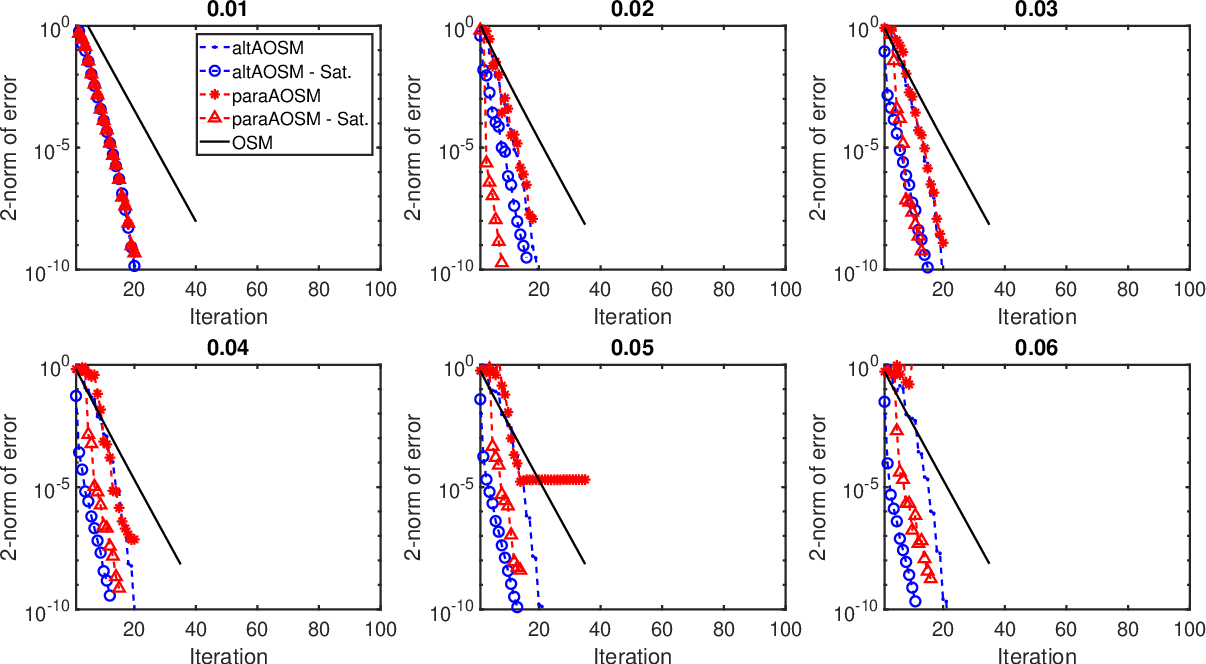
\[ \nabla (\alpha(x,y) \cdot \nabla u(x,y) ) = f(x,y), \quad (x,y) \in \Omega = [-1,1] \times [-1,1], \] \[ u(x,y) = h(x,y), \quad (x,y) \in \partial \Omega, \]
Solve this using FEM software

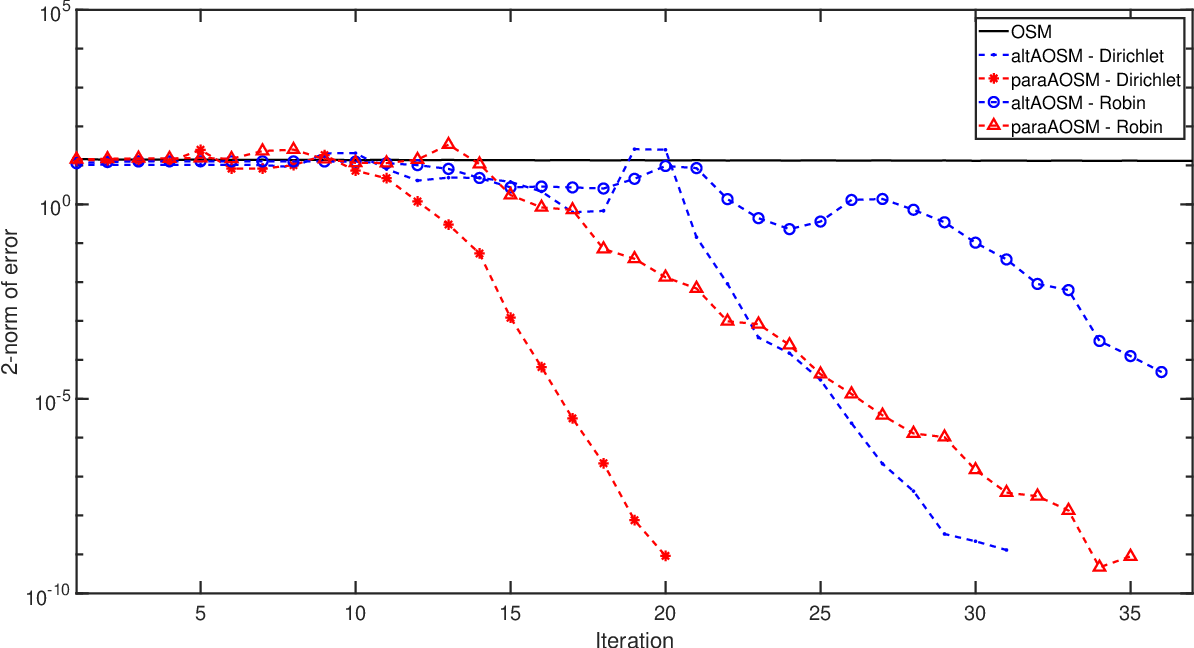
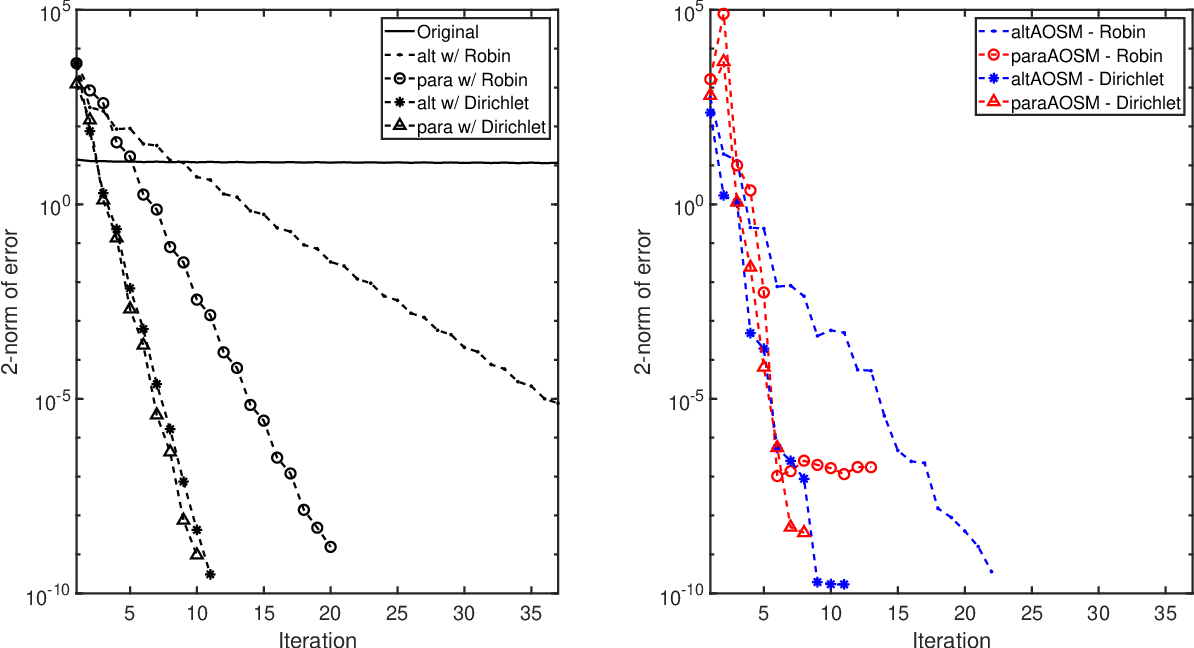
Conclusions
- AOSMs give GMRES convergence without GMRES cost
- Transmission conditions can be re-used, for restarts and time steps
Future work
- Track down stability issues
- Test out other choices of adaptive transmission conditions