Why intersect simplices?

Nonmatching grids

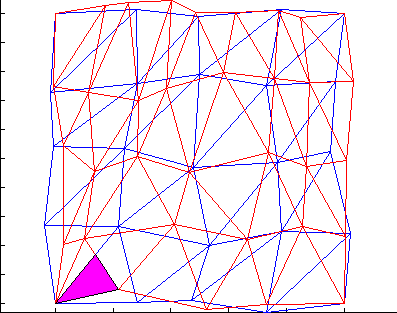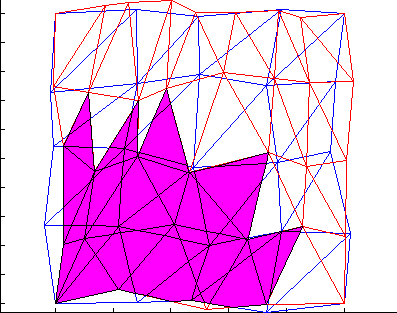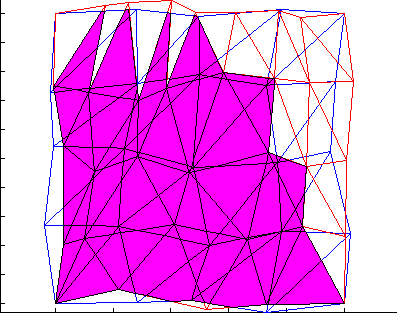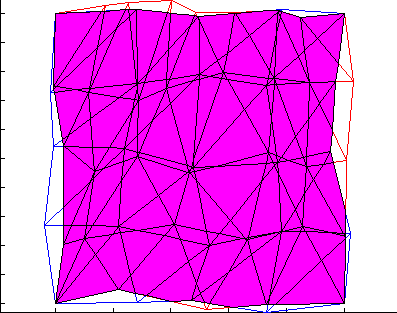
https://www.unige.ch/~gander/demo.php

Clipping

Multiphysics

Parameter estimation

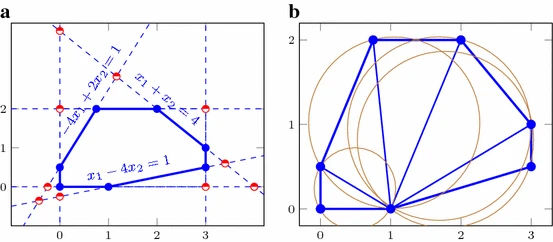
Paulavičius, R., Žilinskas, J. Advantages of simplicial partitioning for Lipschitz optimization problems with linear constraints. Optim Lett 10, 237–246 (2016). https://doi.org/10.1007/s11590-014-0772-4

Sectioning

The intersection of two simplices can be found through successive intersections with hyperplanes

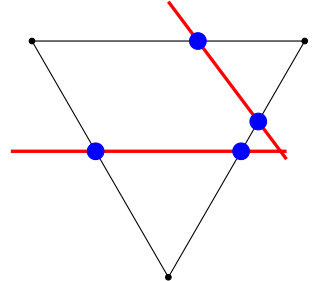
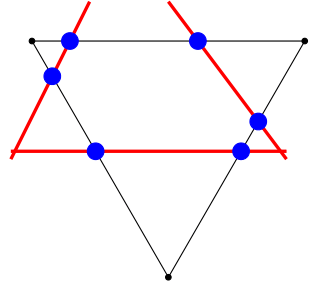
The intersection of two simplices can be found through successive intersections with hyperplanes

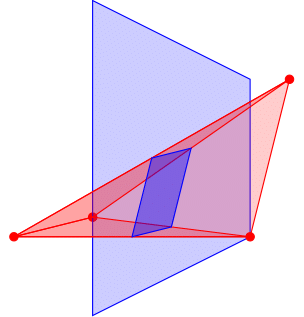
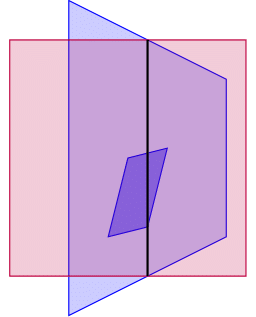
Throughout this presentation, we will focus on two examples: the simplex in 2D and the simplex in 5D

A hyperplane divides vertices into two groups, one on each side

We call the two groups fathers and mothers

Any vertices lying directly on the hyperplane are grouped with the fathers

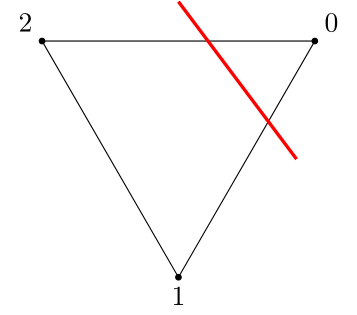
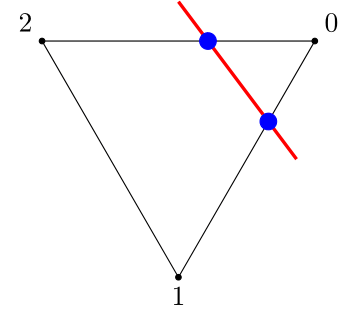
A father and a mother with an edge between them create an intersection (child) with the hyperplane

Not all fathers have children with all mothers, they must neighbour each other

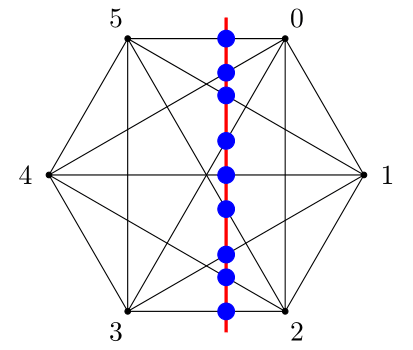
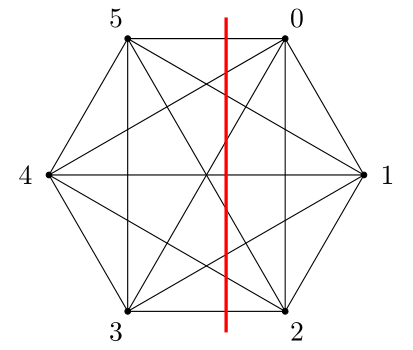
We need to be able to uniquely identify any intersection between simplex and hyperplane

Let each vertex of the simplex have an index from 0 to $n$

Then let the index of the child of any two parents be the union of their indices

1st order sections

sectioning a simplex with one hyperplane

Vertices of a section are the children of a father and a mother

This gives a set of vertices, but not a set of edges

Which children are neighbours in the section?

Two vertices are neighbours if their indices differ by exactly one element

Indices increase by one element after each sectioning

If two children share a parent then their indices share the parent's index and differ by one element

These children, called siblings, are therefore neighbours and have an edge between them

Cross-hatching

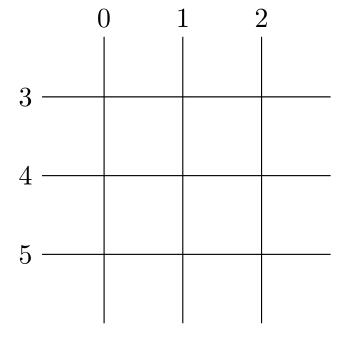
Diagram to help visualize sections

For each father, draw a vertical line

For each mother, draw a horizontal line

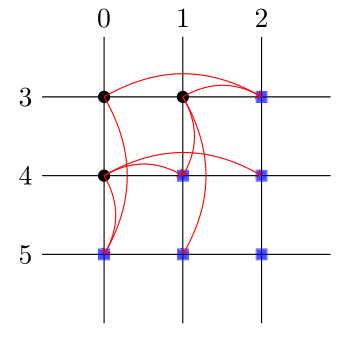
Every intersection is a child in the 1st order section

Any children connected along the same horizontal or vertical line of the cross-hatch are siblings

This means each line represents a simplex

This lets us draw the net of the section

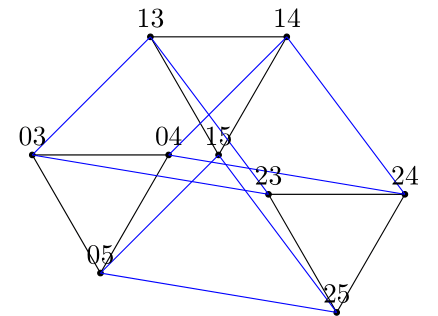
1st order sections are all duoprisms, the Cartesian product of two simplices

2nd order sections

The vertices of the 1st order section are now parents for the 2nd order section

Colour each child in the cross-hatch based on whether it is a father or a mother

Since the section is convex, fathers and mothers are split into contiguous groups

In the cross-hatch diagram, if one can draw a right-angled triangle with vertices a father and two mothers, or a mother and two fathers, then the two children associated with these parents are siblings

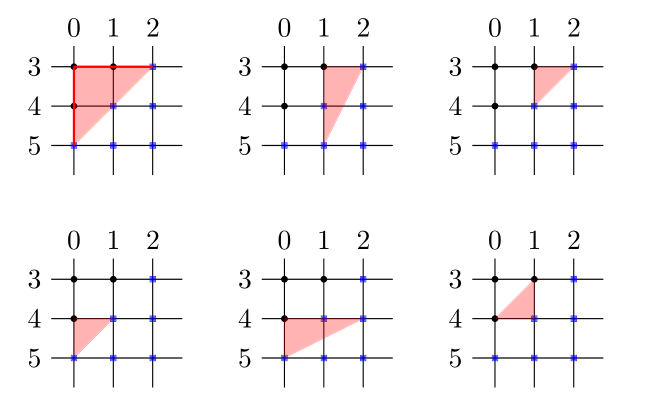
Also, if three parents form a line, then their children are siblings

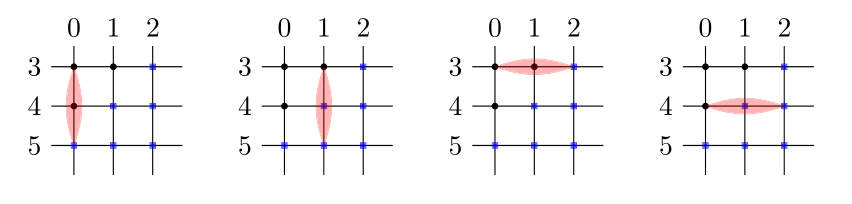
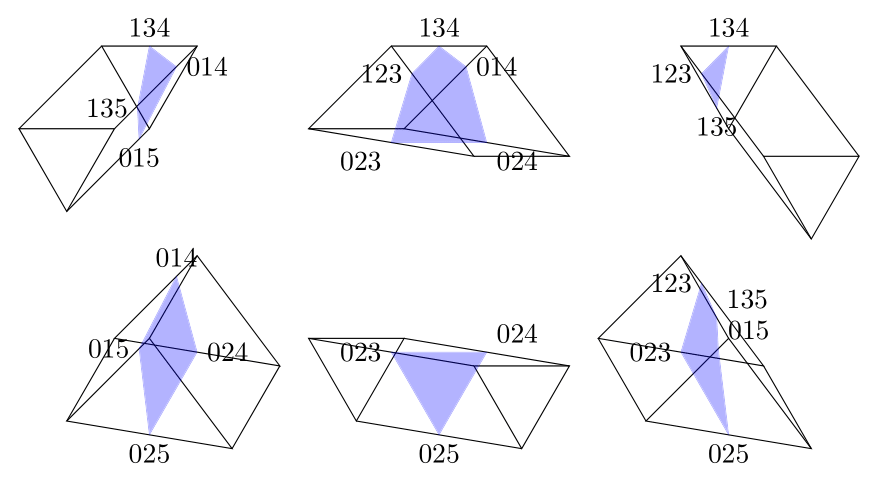
If two children have fathers who are neighbours and mothers who are neighbours, then these chilrden (cousins) are neighbours in sections of order 2 and higher

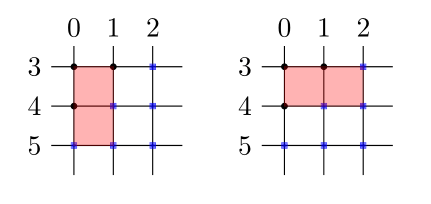
Only siblings and cousins are neighbours in 2nd order sections

If one can draw a rectangle with vertices two fathers and two mothers, then the associated children are cousins

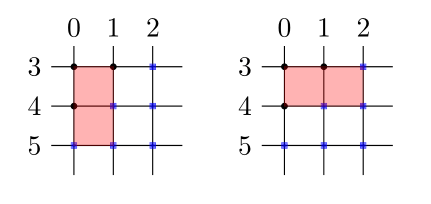
We can draw the net, but it doesn't necessarily help us see the structure

Geometrically, this intersection cuts each cell (3D face) of the 1st order section with a plane

General sections

Vertices whose indices share all but $m$ elements all lie on the same $m$-face of the simplex

Vertices of $k$-th order sections have exactly $n-k$ neighbours

Conclusions

Cross-hatching provides strategies for visualizing the intersection between simplices and hyperplanes

This can help consider problems that might arise in algorithm design and geometric proofs